Prime Factors, HCF and LCM

Finding the highest common factor (HCF) or lowest common multiple (LCM) of a pair of numbers is a common grade C topic occuring on the non calculator of your maths exam. It's normally a two part question and you will need to use your answer to part a) to help answer part b) as you will see in the example below.

Example Question

a) Write 24 as a product of its prime factors.

b)
i) Find the highest common factor (HCF) of 24 and 60.
ii) Find the lowest common multiple (LCM) of 24 and 60.

Solution

a)
To “write as a product of its prime factors” means to write the number as a multiplication sum using only prime numbers. We do this by using a prime factor tree. The number 24 is repeatedly split into factor pairs until only prime numbers are left at the end of the branches.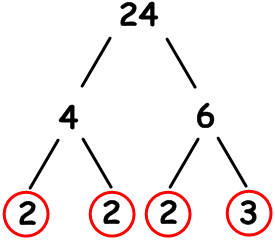

So: 24 = 2 x 2 x 2 x 3
= 2³ x 3

Important – You must remember to write your answer using powers or you will lose a mark!

b)
The second part of this question asks to find the HCF and LCM of 24 and 60. To do this we must also break down 60 into its prime factors just like we did in part a).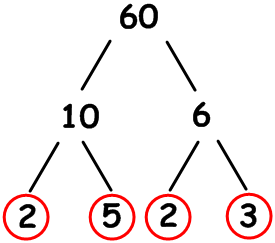

So: 60 = 2 x 2 x 3 x 5
= 2² x 3 x 5

i) The HCF of 24 and 60 is found by comparing the prime factors and multiplying the numbers common to both lists.

24	=	2	x	2	x	2	x	3
60	=	2	x	2	x			3	x	5

So the HCF of 24 and 60 is 2 x 2 x 3 = 12.

ii) The LCM of 24 and 60 is found by multiplying together all the prime factors of both numbers. However if a number occurs in both lists we only count it once.

24	=	2	x	2	x	2	x	3
60	=	2	x	2	x			3	x	5

So the LCM of 24 and 60 is 2 x 2 x 2 x 3 x 5 = 120.

Hint: This sum is easy if you first do 2 x 5 = 10 then 2 x 2 x 3 = 12. Then 12 x 10 =120.

Test Yourself!

Find the HCF of 48 and 72.
Find the LCM of 48 and 72.

back to key topics